2016-2022年中国防伪印刷行业发展现状及前景战略咨询报告 28页

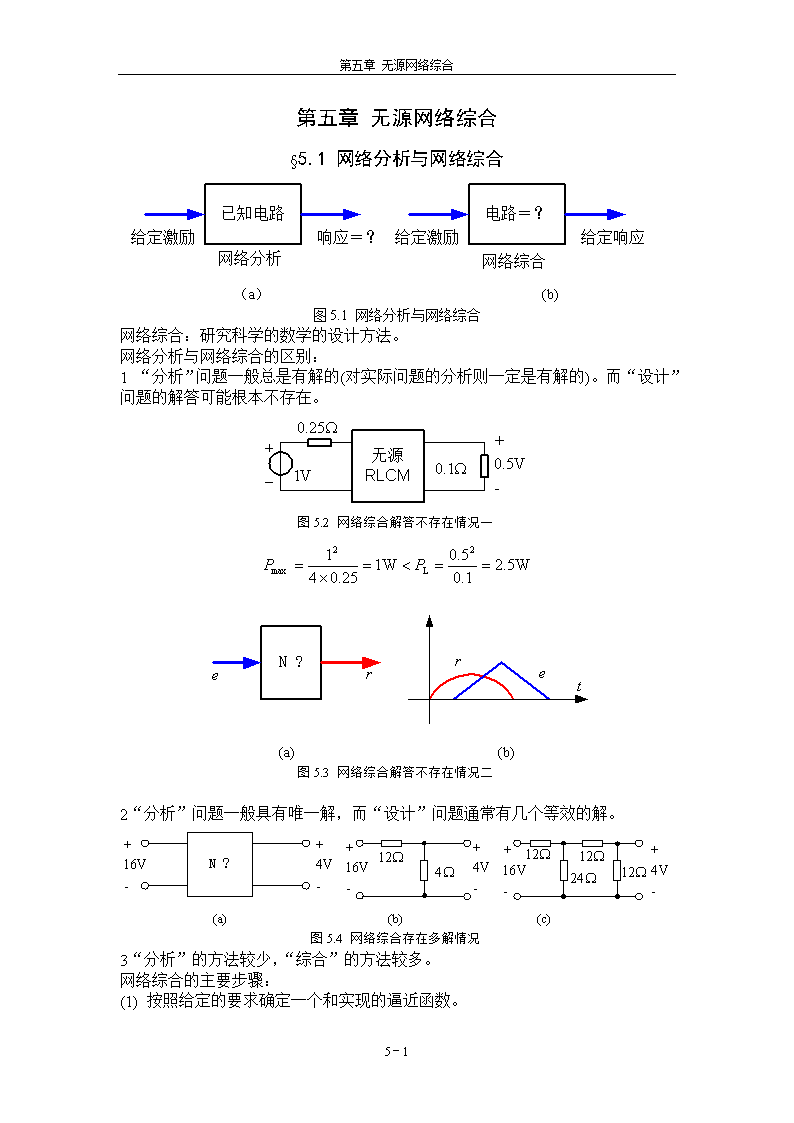
'第五章无源网络综合第五章无源网络综合§5.1网络分析与网络综合（a）(b)图5.1网络分析与网络综合网络综合：研究科学的数学的设计方法。网络分析与网络综合的区别：1“分析”问题一般总是有解的(对实际问题的分析则一定是有解的)。而“设计”问题的解答可能根本不存在。图5.2网络综合解答不存在情况一(a)(b)图5.3网络综合解答不存在情况二2“分析”问题一般具有唯一解，而“设计”问题通常有几个等效的解。(a)(b)(c)图5.4网络综合存在多解情况3“分析”的方法较少，“综合”的方法较多。网络综合的主要步骤：(1)按照给定的要求确定一个和实现的逼近函数。5－28 第五章无源网络综合(2)寻找一个具有上述逼近函数的电路。§5.2网络的有源性和无源性输入一端口网络N的功率从任何初始时刻到，该网络的总能量式中为在初始时刻时该一端口储存的能量。若对所有以及所有时间，有（1）则此一端口N为无源的。如果一端口不是无源的，达就是有源的。就是说，当且仅当对某个激励和某一初始值以及某一时间，有，则此一端口就是有源的。换句话说，如果一个一端口是有源的，就一定能找到某一激励以及至少某一时间，式（1）对这个一端口不能成立。在以上有关无源性的定义中必须计及初始储存能量。例如，对时不变的线性电容，设它的电容值为C，则有式中。所以时，电容元件为无源的，而当时（线性负电容），则为有源的。但是，如不计及式中的初始能量项，则为从到输入网络的能量。这样即使，在某些时间将小于零。事实上充电的电容有可能向外释放储存的能量，但是计及初始能量，它不可能释放多余原先储存的能量。为了考虑这种情况，引入了有关“无损性”的概念。设一端口的所有从为“平方可积”，即有：5－28 第五章无源网络综合如果对任何初始时间，下式成立式中为在初始时刻时该一端口储存的能量，则称此一端口为无损网络。以上关于和平方可积的条件，也即就是说，一端口在和时均为松弛的。假设一端口在时无任何存储能量，则无源性可按下式定义（2）以上关于有源性的定义可以推广到N端口。如果全部端口的电压电流允许信号对是真实的，且对所有，输入端口的总能量为非负的，则此N端口为无源的，即对全部，有这里设时，。如果对某些信号对，且对某些，有则此N为有源的。如果对所有平方可积有限值允许信号对，有则称此N端口为无损的。一个无损的N端口将最终把输入端口的能量全部返回。线性（正）电阻元件、电容元件、电感元件均为无源元件。例如，对二端电阻，按式（2）有可见，只要，对所有，总是非负的。同理，对于非零的和，将是的单调非递减正值函数，因此当时，不可能是零值，所以线性电阻是无源的、非无损的。线性负电阻、负电感、负电容是有源元件。5－28 第五章无源网络综合对于理想变压器，有按式（1－25）所以理想变压器是无源的且是无损的。练习：讨论回转器和负阻抗变换器的有源性和无源性。回转器：，负阻抗变换器：§5.3归一化和去归一化归一化定义：用一些合适的系数(常数)按比例换算所有电量，而不改变电路性质。例如，用50作为电阻的换算系数(归一化常数)，则(实际值)变成(归一化值)。归一化值、实际值、归一化常数之间的关系，，，，，，，对实际值适用的物理关系，对归一化值网络应保持不变，因此得5－28 第五章无源网络综合共七个关系式。综上得知，只有两个独立的归一化常数，若选择多于两个，则有可能破坏电量之间的关系。通常选择和。此时【例】图5.5(a)所示电路归一化电压转移函数为中心角频率为。(1)如要求中心频率为10kHz，求网络函数。(2)如固定，求L，C。(3)如固定C=0.1µF,求R，L。(a)(b)图5.5归一化例题图【解】：(1)频率归一化常数为将代入已知的得：(2)µH，µF(3)5－28 第五章无源网络综合§3.4正实函数1定义设是复变量的函数，如果(1)当时，；(2)当时，。则称为正实函数，简称PR函数。正实函数的映射关系如图5.6所示。2正实函数的性质(1)F(s)的全部极点位于s平面的闭左半平面，F(s)在s的右半平面是解析的。证明思路：设F(s)在s的右半平面存在极点，级数展开，F(s)变号，与正实函数矛盾，假设不成立。(2)位于轴上的极点是一阶的，且其留数为正实数。(包括0和±∞)(3)正实函数的倒数仍为正实函数(对正实函数的零点也做了规定)。(4)设。则，。因为，在和处为一阶极点(零点)。3布隆定理(OttoBrune1931年提出)（a）(b)5－28 第五章无源网络综合图5.7布隆定理的证明对图5.7(b)，定理：当且仅当Z(s)是s的正实函数时，阻抗函数Z(s)使用集中参数的RLCM元件(非负值)才是可实现的。必要性的证明：(充分性留在后续各节)(5.1)其中由式(5.1)得(1)当时，。(2)设则所以Z(s)是正实函数。5－28 第五章无源网络综合4等价的正实条件一(1)当s为实数时，F(s)也是实数；(2)对全部实频率，；(3)F(s)的全部极点位于s平面的闭左半平面，位于轴上的极点是一阶的，且具有正实留数。以Z(s)为例解释如下：(1)。所以Z(s)中的系数一定是实数，即Z(s)是s的有理实函数。(2)在正弦稳态下，一端口的等效电路为它消耗的平均功率为(因为是无源网络)所以。(1)设，即，则冲激响应电压为若或，则发散；若(位于轴上)，则对应高阶极点的响应项发散。以上对无源RLCM网络是不可能的。5等价正实条件二设(1)M(s)、N(s)全部系数大于零；(2)M(s)、N(s)的最高次幂最多相差1，最低次幂最多也相差1；(3)F(s)在轴上的极点是一阶的，且具有正实留数；(4)；(5)M(s)、N(s)均为Hurwitz多项式。[例]5.1判断下列正实函数是否为正实函数。5－28 第五章无源网络综合(a)；(b)[解](a)显然满足(1)、(3)。又，满足(2)，是正实函数。(b)显然满足(1)、(3)。但。不是正实函数。§5.5LC一端口的实现LC一端口：一或的性质1在s=0处或是一零点或是一极点。。端口处要么等效为短路，要么等效为断路。分别对应的零点和极点。2在处或是一零点或是一极点。解释同上。3Z(s)的全部极点和零点位于轴上。(因此是一阶，留数大于零)LC一端口，R=0，冲激响应不衰减(因为无损)，等幅振荡，故全部极点位于轴上。的零点就是的极点，也应位于轴上。极点(零点)成对出现。4为s的奇函数，即。解释(1)5－28 第五章无源网络综合N(s)、D(s)或为奇函数或为偶函数。(2)P(s)为偶函数→为实数；P(s)为奇函数→为虚数。(1)，纯虚数，电抗性质。所以N(s)、D(s)必为一偶一奇→Z(s)为s的奇函数。5Z(s)的零、极点交替出现在轴上。示意图如下：(a)5－28 第五章无源网络综合(b)图5.10LC导抗函数的零极点分布图综上得LC导抗函数的充要条件：1Z(s)或Y(s)为正实函数；2零、极点均位于轴上且交替出现。二LC一端口的Foster综合(基于部分分式展开)1Foster第一种形式[串联形式，用Z(s)]图5.11LC导抗函数的Foster第一种综合形式2Foster第二种形式[并联形式，用Y(s)]5－28 第五章无源网络综合图5.12LC导抗函数的Foster第二种综合形式【例】5.2分别用Foster第一和第二种形式综合阻抗函数【解】(1)对Z(s)进行展开图5.13例题5.2的Foster第一种综合形式(2)对Y(s)进行展开5－28 第五章无源网络综合图5.14例题5.2的Foster第二种综合形式三Cauer(考尔)综合(基于连分式)1Cauer第一种形式(特点：逐次移出处的极点。串臂为电感，并臂为电容)【例】5.3设。试用Cauer第一种形式综合。【解】为Z(s)的零点，故首先用Y(s)。使用长除运算得到上式。(多项式按降幂排列)2Cauer第二种形式(特点：逐次移出s=0处的极点。串臂为电容，并臂为电感)5－28 第五章无源网络综合例5.4设。试用Cauer第二种形式综合。【解】使用长除运算得到上式。(多项式按升幂排列)图5.18练习1试确定下列驱动点阻抗函数能否用LC一端口来实现？5－28 第五章无源网络综合2试用Foster两种形式综合阻抗函数。3试用Cauer两种形式综合阻抗函数。4设计一个LC一端口网络，要求时，阻抗为零；时，阻抗为无限大；时，阻抗为200Ω。参考答案235－28 第五章无源网络综合§5.6RC一端口的实现一RC一端口的性质(必要条件)1所有零极点位于负实轴上，而且是一阶的。解释：若不位于实轴→冲激响应振荡→同时存在LC元件；若位于正实轴→冲激响应发散。以上对无源RC网络是不可能的。证明：（1）位于负实轴：,,令得,令得(2)零极点是一阶的5－28 第五章无源网络综合(设为n阶极点，则时，。令，得故图5.192极点留数为正实数(它们与R、C值成比例)3最低的临界频率(即最靠近原点的零极点)为极点，原点处要么是极点，要么是常数。(a)(b)图5.204最高的临界频率为零点，在处要么为零点，要么为常数。5零极点交替出现在负实轴上。5－28 第五章无源网络综合图5.21RC阻抗函数的零极点分布二Y(s)的性质1全部零极点位于负实轴上，而且是一阶的。2Y(s)的极点留数为负实数，而Y(s)/s的极点留数为正实数。3最低的临界频率为零点。4最高的临界频率为极点。5零极点交替出现。三Foster综合(基于部分分式展开)1Foster第一种形式(并串联形式)图5.22Foster第一种综合形式Foster第二种形式(串并联形式)展开得[因为，所以对进行展开。]5－28 第五章无源网络综合图5.23Foster第二种综合形式【例】5.5试用Foster两种形式综合。【解】(1)Foster第一种形式展开(2)Foster第二种形式展开图5.24例题5.5图四Cauer型综合(基于连分式)1Cauer第一种形式(串臂为电阻，并臂为电容)，由Z(s)性质4得图5.25Cauer第一种形式多项式用降幂排列。2Cauer第二种形式(串臂为电容，并臂为电阻)。由Y(s)性质3得5－28 第五章无源网络综合图5.26Cauer第二种形式多项式用升幂排列【例】5.6试用Cauer两种形式综合。【解】(1)Cauer1图5.27用Cauer1综合结果Cauer25－28 第五章无源网络综合图5.28用Cauer2综合结果练习1试确定下列驱动点阻抗函数那些能用RC一端口来实现？(a);(b)；(c);(d)。2试用Foster两种形式综合RC阻抗函数5－28 第五章无源网络综合3试用Cauer两种形式综合RC导纳函数4一个阻抗函数的零极点分布如图5.29所示，。试用梯形电路实现此函数。图5.29§5.7RLCM一端口的实现一定义1不含轴上极点的阻抗(导纳)函数，称为极小电抗(电纳)函数。2在轴上某一点具有零实部的阻抗（导纳）函数，称为极小实部函数；3如果一个导抗函数同时是极小电抗函数、极小电纳函数，极小实部函数，则称之为极小函数。（极小函数是正实函数）。示例极点(极小电抗函数)，零点5－28 第五章无源网络综合(极小电纳函数)。（极小实部函数）。二从正实函数中分解出极小函数1移出轴上的极点：设移出上的极点：,(在轴上无零极点)。2电阻约简（移出实部最小值）。当时，---极小函数。图5.28从正实函数中分解出极小函数示例三极小函数的布隆综合设为极小函数，则存在，使得。1以情况为例：提取串联元件，使余函数,即要求。5－28 第五章无源网络综合(1)设串联元件为电容，则。进一步分析如下：(a)在s=0处存在极点，且极点留数为-1/C1<0,Z2(s)不是正实函数。(b)Z1(s)=Z2(s)+1/(sC1)在s=0处存在极点，Z1(s)非极小函数，矛盾。故串联元件不能为电容。(2)设串联元件为电感，则(a)两个正实函数之和仍为正实函数。在处存在零点(一定成对出现)，移出之图5.29(b)，时，，图5.30仍为正实函数，化为极小函数后重复上述过程。在处无极点。（c）解决负电感问题5－28 第五章无源网络综合学习电路等效变换：图5.31可实现的必须满足条件：(1)由图5.30得当时，(为有限值)因为是极小函数，在处无极点，所以验证条件（1）全部满足条件(1)。【例】5.7设。试综合之。【解】1移出轴上的极点。5－28 第五章无源网络综合,,2电阻约简，令得,-------极小函数3，(为零点)4，，5，，图5.32消去负电感后得5－28 第五章无源网络综合图5.332时，与对偶图5.34消去负电感。图5.35练习1试综合。参考答案：5－28 第五章无源网络综合2试综合。参考答案：5－28'